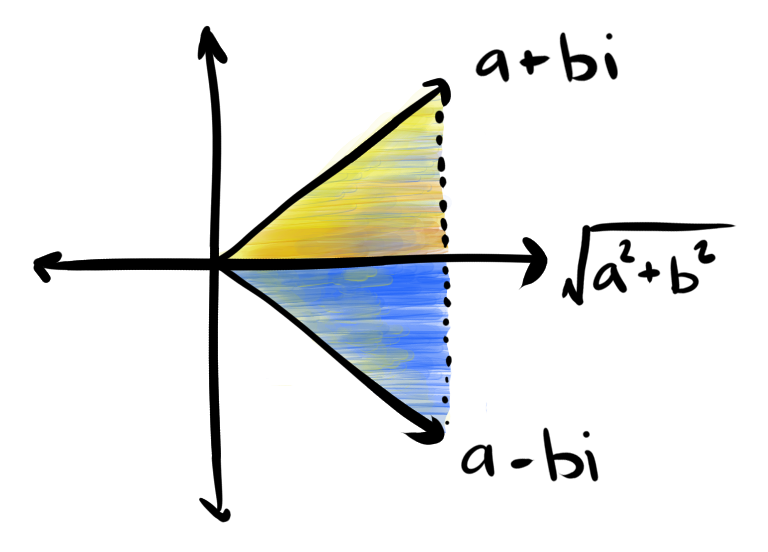Quaternions From Scratch

Now, let's suppose that there is second dimension, just like the first, and we're free to move in either dimension independently. What happens when we move in both directions at the same time? The answer depends on what kind of space we're in, and here we're assuming we're in good old-fashioned Euclidean space, where the pythagorean theorem holds:

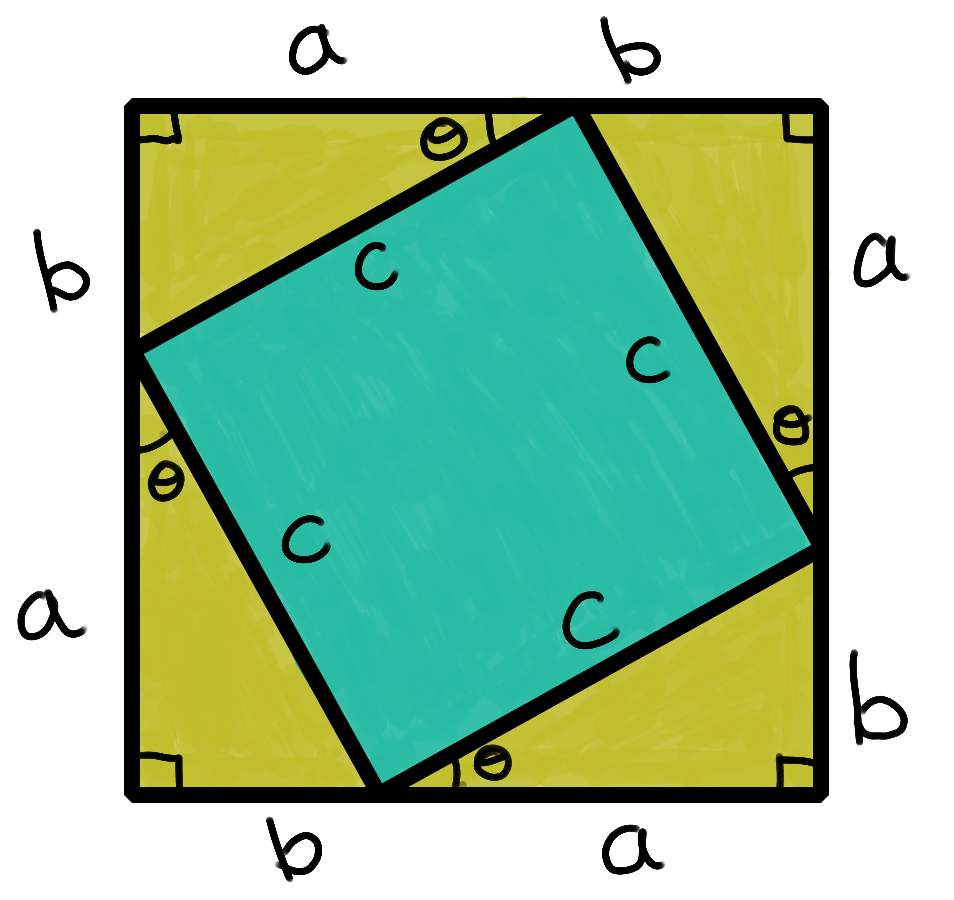
This means that moving along the first dimension for a distance of and along the second dimension for a distance of results in the same position as moving a distance of straight toward the final position. The theorem tell us how to translate away from the origin at an angle and modulus :

The angle is sometimes referred to as the "argument", apparently coming from its uses in astronomy for measuring celestial positions. The root of "argue" means "to shine", as if a verbal argument shines light on an issue and an angle argument tracks the motion of shiny celestial objects.

So now that we can point in any combination of two directions, what have we lost? We've lost the ability to order all the points along a single line. We can still order the points along a given direction, but not in general.

But then how do we think about the actual action of rotation? How do we take a point from where we got by going along one direction, to where we would have gotten had we gone in another direction? Similar to taking the inverse in 1 dimension, but we want to be able to go in any combination of 2 directions.

In order to rotate, there two basic behaviors we have to capture. The first is easy, staying in the same direction. We already know how to do that: multiply by , our affirming friend, the identity element. The other is to rotate, that is, to shift our position from one dimension to the other. This is similar to reflecting between opposites along the same dimension, but shifting to another instead.

We can understand the essence of rotation to be going from pointing in one direction to pointing in another. To model this movement we can start by exchanging the two dimensions. In other words, we can take the point to the point , equivalent to reflecting across the line . This takes , which we want, but also takes , which is in the wrong direction! We need a second movement to flip around and get all four going in a cycle. I recommend trying this two-step operation with a piece of paper, flipping it across its diagonal and then horizontal, just to get a tangible feeling for how these two flips rotate the page a quarter turn.

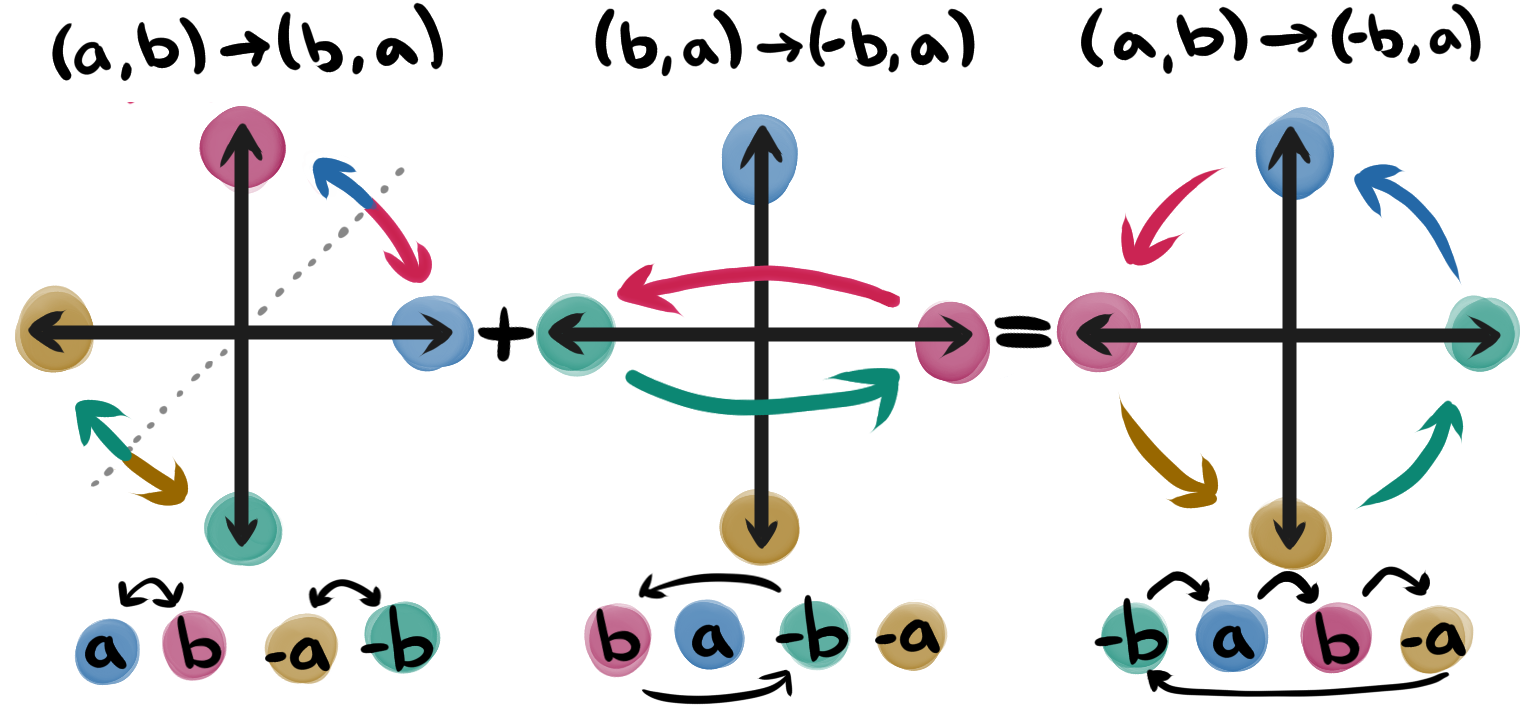
Let's briefly compare these two reflections. The first reflection involves swapping the components. The effect it has on a given position depends on the distance between its components. If one part of the journey to was longer than the other, which was longer gets swapped.

This gets combined with the second reflection, which negates only the first coordinate. Notice that this changes the effect of the first reflection the next time around, e.g. if the components were in the same direction, now they are in opposite directions.

Normally, repeatedly negating a number causes it to alternate between plus and minus in a 2-step cycle, but now the number is getting swapped out each time and two separate numbers are going through the 2-step cycle independently. Therefore the full cycle takes 4 rather than 2. Try it out here:

If we reverse the order of the reflections, the first component gets negated before getting swapped, causing the rotation to move in the opposite direction. This operation is called the conjugate, meaning "joined together". Notice that applying a rotation and then applying its conjugate will do and then undo the reflections in the reverse order. They are inverse operations.

Now that we know both how to stay in place and go in a cycle , we can transition between them according to the pythagorean theorem:

Each component in the resulting position is itself composed of two terms, one that stayed in place and one that cycled in from the other component. This combination captures the rotational behavior.

Therefore, similar to the 1 dimensional case, we have two aspects of translations in 2 dimensions, namely "which direction?" and "how far?" The domain of direction has expanded from facing forward or backward, , to being able to turn around (here in either direction), . Notice that turning around to face backward can no longer be considered a simple reflection across the first dimension, but rather all points in the plane of rotation invert through the origin so that "left" and "right" dont get mirrored. Rotating turns around via two reflections, not one. Try taking a spin below:

The word "complex" means "folded together". The complex numbers enfold this 4-way cycle into a piece of mathematical origami called an algebra. The word "algebra" is associated with creating symbolic systems that encode rules and operations, and we would like to be able to combine and manipulate rotations in singular equations, without having to break them up into individually defined components. In order for the complex numbers to keep track of the two actions of staying and rotating, it needs a variable for each one.

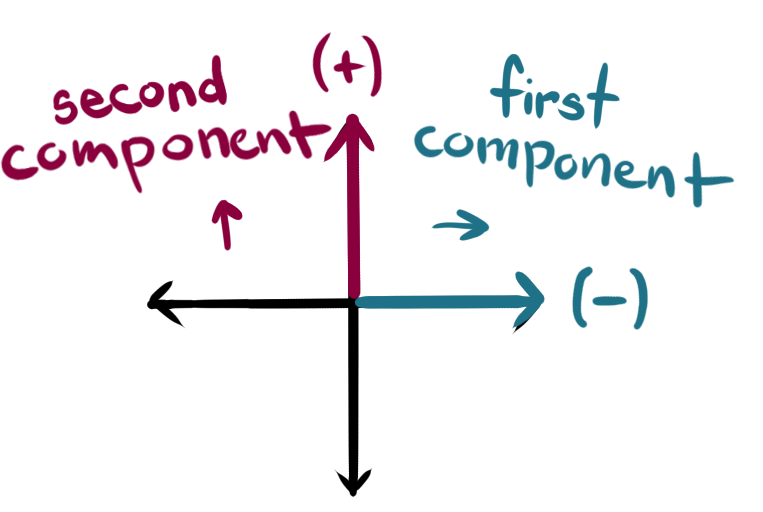
Consider that a point in 2D has two interpretations. First, as position coordinates, and secondly, as an action composed of a translation and a rotation. When we consider a rotation on its own, the first component represents the stay (or reverse) behavior, while the second component represents the cycle behavior. Together they must make a triangle with hypotenuse length so as not to cause any scaling.

We already have a symbol for the stay behavior, our old friend the identity element, . Now we need an element to capture the cycle behavior. The standard notation is to use the letter , which will act a marker representing the second component:

If we multiply by itself, that is, take we see it gives the expected behavior of . Now we can relabel the picture above, substituting in our algebraic representation:

Each component is made of a part that stayed and a part that cycled.

Previously, we noted that reversing the order of reflections causes rotations to reverse, which is called the conjugate. Since captures the cycling behavior in our algebra, negating the component causes the rotation to move in the opposite direction, equivalent to reversing the order of reflections. When multiplied by its conjugate, the rotations represented by complex numbers cancel out, resulting in a point on the real number line.

Since complex numbers are a form of multiplication, and division is the inverse of multiplication, conjugation, which undoes the rotation, is a sort of division on rotations. It undoes the action of its conjugate:

Notice that multiplying by the conjugate is giving us back the relationship that we started with when we first moved to two dimensions, the pythagorean theorem. By undoing any sort of rotation we've ended up back in 1 dimension. All we have to do from here to get the original value of is to take the square root. This distance from the origin is sometimes called the "Euclidean norm", where "norm" is a generalized term for distances and magnitudes. In broader contexts, the euclidean distance, calculated by summing the squares of the components, is referred to as the norm ( named after Lebesgue).